Educational CF Round 91 Summary

Educational CF Round 91 Summary(2020-7-12 20:35-1:05)

xiaoh 2020-7-17

题目链接

A-Three Indices

题意

给定一个$1-n$的排列$p$,求三元组$(i,j,k)$满足$p_j>p_k,p_j>p_i$或判断其不存在。

数据范围：

$T\leq 200,3\leq n\leq 1000,1\leq p_i\leq n$

题解

本质上就是求一个单调上升后单调下降的序列是否存在，直接开一个$bool$判断之后输出即可。复杂度$O(n)$

Code

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=1010;
int n;
int a[MAXN];
int main()
{
	int t;
	read(t);
	while(t--)
	{
		read(n);
		for(int i=1;i<=n;++i) read(a[i]);
		int flag=0;
		int x=0,y=0,z=0;
		for(int i=2;i<=n;++i)
		if(a[i-1]<a[i])
		{
			if(flag==0) flag=1,x=i-1;
		}
		else if(a[i-1]>a[i])
		{
			if(flag==1)
			{
				y=i-1;
				z=i;
				cout<<"YES"<<endl;
				cout<<x<<" "<<y<<" "<<z<<endl;
				goto ending;
			}
		}
		cout<<"NO"<<endl;
		ending:;
	}
	return 0;
}

B-Universal Solution

题意

给定一个由$R,S,P$组成的字符串$S$，每个字符分别表示石头剪刀布中的石头，剪刀，布。对手将从某个位置开始环形地出手势，一共出$|S|$次。对手对于每个位置的选择是等概率的。现在你需要固定你出招的序列$c$，使这个序列的胜利次数的期望着最大。求$c$。

数据范围：

$t\leq 1000,|c|=|S|\leq \sum |S|\leq 2\times 10^5$

题解

显然，我们可以将期望值转化为如下式子：

$exp(c)=\frac{1}{|S|}\sum_{i=0}^{|S|}\sum_{j=0}^{|S|} judge(s_i,c_j)$

我们可以理解为每一个$c_j$都与整个$|S|$比赛一轮，然后最大化这个赢的次数。显然，选择$|S|$中出现最多的一个手势，然后每一个$c_j$都选择战胜它的那个手势，可以最大化$\sum$里面的值。直接输出即可。复杂度$O(n)$

Code

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=200010;
int n;
char ch[MAXN];
int main()
{
	int t;
	read(t);
	while(t--)
	{
		scanf("%s",ch+1);
		n=strlen(ch+1);
		int cntr=0,cnts=0,cntp=0;
		for(int i=1;i<=n;++i)
		if(ch[i]=='R') ++cntr;
		else if(ch[i]=='S') ++cnts;
		else ++cntp;
		if(cntr>=cnts&&cntr>=cntp)
		{
			for(int i=1;i<=n;++i) putchar('P');putchar('\n');
		}
		else if(cnts>=cntr&&cnts>=cntp)
		{
			for(int i=1;i<=n;++i) putchar('R');putchar('\n');
		}
		else
		{
			for(int i=1;i<=n;++i) putchar('S');putchar('\n');
		}
	}
	return 0;
}

C-Create The Teams

题意

有$n$个人，每个人都有一个技能职值$a_i$。现在需要选将其分为一些队伍，每支队伍的人数$\times$队伍中$a_i$的最小值必须至少为$x$。求至多能分为几队。

数据范围

$t\leq 1000,n\leq \sum n\leq 10^5,1\leq a_i,x\leq 10^9$

题解

显然，通过微扰法可证明每次选择的队伍都为连续的一段时最优。将整个序列排序，然后不停地往一个队列里加人直到满足条件后关闭这个队伍，新开一个队伍继续塞即可。复杂度$O(n\log n)$。

Code

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=100010;
int n,x;
int a[MAXN];
int main()
{
	int t;
	read(t);
	while(t--)
	{
		read(n),read(x);
		for(int i=1;i<=n;++i) read(a[i]);
		sort(a+1,a+n+1),reverse(a+1,a+n+1);
		int ans=0;
		int cnt=0;
		for(int i=1;i<=n;++i)
		{
			++cnt;
			if(cnt*a[i]>=x) cnt=0,++ans;
		}
		write(ans),putchar('\n');
	}
	return 0;
}

D-Berserk And Fireball

题意

给定一个长度为$n$的无重复序列$a$和一个长度为$b$的序列$b$，现有两种法术：

1. Fireball:可以消灭连续$k$个数字，代价为$x$；
2. Berserk:可以使大的数字消灭相邻的小的数字，代价为$y$。

求使序列$a$变为序列$b$的最小代价，或判断其不可行。

数据范围：

$1\leq m\leq n\leq 2\times 10^5,1\leq x,y\leq 10^9,1\leq k\leq n,1\leq a_i,b_i\leq n$

题解

由于序列不可重，所以对应模式固定，若无对应则无解。

对应后，匹配的数将不匹配的数分割成了一些段，显然不同段直接不能跨段操作。所以我们将其分开考虑。记这个段的长度为$len$，最大的数为$p$。当$p>l$且$p>r$时，则最大的一个数必须被fireball干掉，所以当$len<k$时无解，否则使用一定次数的berserk（至少$len\bmod k$次），然后用fireball干掉其他的即可。注意必须使用一次fireball。可以通过费用$O(1)$计算。

当$p<max(l,r)$时，则两端可以一直通过berserk杀光中间的数字，也可以先用berserk再用fireball处理，同上根据费用取较小者即可。复杂度$O(n)$。

Code

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=200010;
int n,m;
long long k,x,y;
int a[MAXN],b[MAXN];
int f[MAXN];
long long ans=0;
inline long long calc(int l,int r)
{
	if(l>r) return 0;
	int maxn=0;
	for(int i=l;i<=r;++i) maxn=max(maxn,a[i]);
	long long cnt=r-l+1;
	if(maxn>a[l-1]&&maxn>a[r+1])
	{
		if(r-l+1<k) return -1;
		return min(x*(cnt/k)+y*(cnt%k),x+y*(cnt-k));
	}
	else return min(y*cnt,x*(cnt/k)+y*(cnt%k));
}
int main()
{
	read(n),read(m);
	read(x),read(k),read(y);
	for(int i=1;i<=n;++i) read(a[i]);
	for(int i=1;i<=m;++i) read(b[i]);
	int l=1,r=1;
	for(int i=1;i<=m;++i)
	{
		while(a[r]!=b[i]&&r<=n) ++r;
		if(a[r]!=b[i])
		{
			printf("-1\n");
			return 0;
		}
		long long tmp=calc(l,r-1);
		if(tmp==-1)
		{
			printf("-1\n");
			return 0;
		}
		ans+=tmp,l=r+1;
	}
	long long tmp=calc(l,n);
	if(tmp==-1)
	{
		printf("-1\n");
		return 0;
	}
	ans+=tmp;
	printf("%lld\n",ans);
	return 0;
}

E-Merging Towers

题意

有$m$座塔,编号为$1-n$的圆环，每座塔上从上到下按照从小到大的顺序套了一些圆环。第$i$个圆环在第$t_i$座塔上。每次可以将一座塔上面连续的一段圆环移到另一座塔上，但是不能破坏塔的性质。记一个局势的困难度为将所有圆盘放到同一根柱子上所需的操作次数。现有$m$个询问，每次会将$a_i,b_i$所在的塔合并。求合并后的困难度。注：每次询问将会保留。

数据范围：

$2\leq m\leq n\leq 2\times 10^5,a_i,b_i保证操作前不在同一座塔上$

题解

经过观察，我们发现困难度即为数对$(i,i+1)$不在同一座塔上的数量。证明显然。

接下来考虑如何维护。现有两种做法，可以用启发式合并粗暴的在线求解，也可以用$Kruskal$重构树来进行处理。

启发式合并难度较小在此不再赘述。我们着重说明一下重构树的解法。

首先，离线，以塔为叶子节点，操作的时间戳为键值建树，则对于每一个数对$(i,i+1)$，在$T_i,T_{i+1}$合并前都将对答案有$1$的贡献。而通过查询两点的$lca$可以快速得到合并的时刻。于是直接跑倍增的$lca$即可。复杂度$O(n\log m)$

啥？你说要树状数组维护贡献？其实一个差分就可以啦！

Code

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=200010,LOGN=20;
int n,m;
int t[MAXN];
int tot=1;
int edge[MAXN*2],nxt[MAXN*2],hd[MAXN*2];
inline void add_edge(int u,int v)
{
	edge[tot]=v,nxt[tot]=hd[u],hd[u]=tot++;
}
int LCA[MAXN*2][LOGN],d[MAXN*2];
queue<int> q;
int logn;
inline void prework()
{
	logn=log2(2*m-1)+1;
	q.push(2*m-1),d[2*m-1]=1;
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=hd[x];i;i=nxt[i])
		{
			int y=edge[i];
			d[y]=d[x]+1;
			LCA[y][0]=x;
			q.push(y);
			for(int j=1;j<=logn;++j) LCA[y][j]=LCA[LCA[y][j-1]][j-1];
		}
	}
}
inline int query(int x,int y)
{
	if(d[x]<d[y]) swap(x,y);
	for(int i=logn;i>=0;--i)
	if(d[LCA[x][i]]>=d[y]) x=LCA[x][i];
	if(x==y) return x;
	for(int i=logn;i>=0;--i)
	if(LCA[x][i]!=LCA[y][i]) x=LCA[x][i],y=LCA[y][i];
	return LCA[x][0];
}
struct node{
	int a,b;
}a[MAXN];
struct Union_find{
	int f[MAXN*2];
	inline void init()
	{
		for(int i=1;i<=2*n;++i) f[i]=i;
	}
	int find(int x)
	{
		return f[x]=(x==f[x])? f[x]:find(f[x]);
	}
}g;
int ans[MAXN];
int main()
{
	read(n),read(m);
	for(int i=1;i<=n;++i) read(t[i]);
	g.init();
	for(int i=1;i<m;++i)
	{
		read(a[i].a),read(a[i].b);
		add_edge(m+i,g.find(a[i].a)),add_edge(m+i,g.find(a[i].b));
		g.f[g.find(a[i].a)]=g.f[g.find(a[i].b)]=m+i;
	}
	prework();
	for(int i=1;i<n;++i)
	{
		int x=t[i],y=t[i+1];
		int tmp=query(x,y);
		++ans[0],--ans[max(tmp-m,0)];
	}
	for(int i=1;i<m;++i) ans[i]+=ans[i-1];
	for(int i=0;i<m;++i) write(ans[i]),putchar('\n');
	return 0;
}

F-Strange Addition

题意

现在我们重定义加法的计算方式，列竖式，对应位数相加，并将答案写在正下方，最终所有数字连在一起为答案。具体栗子如下：

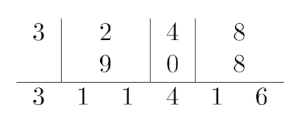
给定算式的结果$c$，且有$n$位。现有$m$次操作，每次修改数位上的一个数字，求每次修改后满足$a+b=c$的$c$的数对的数量。要求对$998244353$取模

数据范围

$1\leq n,m\leq 5\times 10^5$

题解

在无修改的情况下，我们可以考虑用线性$dp$来进行解决。用$f_i$表示构成$c$前$i$位的加法算式的数量。那么每次可以在两个算式后面各加一位，使其成为$c_{i+1}$或$c_{i+1}c_{i+2}$。粗暴的统计即可。

那么考虑如何使其支持修改。不妨用线段树进行维护。我们维护每个区间计算/不计算第一位，计算/不计算最后一位，共四种情况下的可能种数。每次合并时从两个子区间合并信息，若两个区间的衔接处可以构成一个$c_{i+1}c_{i+2}$，那么我们需要加上这种情况下的情况总数。具体的转移方程可以参考代码内的过程。总的复杂度为$O(m\log n)$，当然常数会比较大，不过时间很充裕能够通过。

Code

#include<bits/stdc++.h>
#define len(p) (f[p].r-f[p].l+1)
#define lp (p<<1)
#define rp (p<<1|1)
#define mod 998244353
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
inline long long mul(long long a,long long b)
{
	return a*b%mod;
}
inline long long add(long long a,long long b)
{
	return (a+b)%mod;
}
const int MAXN=500010;
int n,m;
char s[MAXN];
int a[MAXN];
struct node{
	int l,r;
	long long val[4];
}f[MAXN*4];
inline void pushup(int p)
{
	int na=len(lp)==1? 0:1;
	int nb=len(rp)==1? 0:2;
	f[p].val[0]=mul(f[lp].val[na],f[rp].val[nb]);
	f[p].val[1]=mul(f[lp].val[na],f[rp].val[3]);
	f[p].val[2]=mul(f[lp].val[3],f[rp].val[nb]);
	f[p].val[3]=mul(f[lp].val[3],f[rp].val[3]);
	int x=a[f[lp].r],y=a[f[rp].l];
	if(x==1)
	{
		int na=len(lp)==1? 2:0;
		int nb=len(rp)==1? 1:0;
		f[p].val[na+nb]=add(f[p].val[na+nb],mul(mul(f[lp].val[0],f[rp].val[0]),19-(10*x+y)));
		f[p].val[na+1]=add(f[p].val[na+1],mul(mul(f[lp].val[0],f[rp].val[1]),19-(10*x+y)));
		f[p].val[2+nb]=add(f[p].val[2+nb],mul(mul(f[lp].val[2],f[rp].val[0]),19-(10*x+y)));
		f[p].val[3]=add(f[p].val[3],mul(mul(f[lp].val[2],f[rp].val[1]),19-(10*x+y)));
	}
}
void build(int p,int l,int r)
{
	f[p].l=l,f[p].r=r;
	if(l==r)
	{
		f[p].val[0]=1,f[p].val[3]=a[l]+1;
		return;
	}
	int mid=(l+r)>>1;
	build(lp,l,mid),build(rp,mid+1,r);
	pushup(p);
}
void modify(int p,int x,int y)
{
	if(f[p].l==f[p].r)
	{
		f[p].val[3]=y+1;
		return;
	}
	int mid=(f[p].l+f[p].r)>>1;
	if(x<=mid) modify(lp,x,y);
	else modify(rp,x,y);
	pushup(p);
}
int main()
{
	read(n),read(m);
	scanf("%s",s+1);
	for(int i=1;i<=n;++i) a[i]=s[i]-'0';
	build(1,1,n);
	for(int i=1;i<=m;++i)
	{
		int x,y;
		read(x),read(y);
		a[x]=y;
		modify(1,x,y);
		write(f[1].val[3]),putchar('\n');
	}
	return 0;
}

G-Circular Dungeon

题意

给定$n$个正整数$c_i$，表示$n$个金库的价值。有两种金库：

1. regular：玩家通过会拿取该点的价值后进入下一个点；

2. mimic：玩家会立刻死亡。

现在你需要将所有金库围成一个圈，第$i$个金库仅能与通向第$i+1$个，你可以任意的安排金库的位置和类型。玩家会从任意一个点进入，一直沿着唯一的路径走知道死亡。现要求你对于$k\in [1,n]$，求恰有$k$个mimic类型的金库时，玩家获得价值期望的最小值。

数据范围

$2\leq n\leq 3\times 10^5,1\leq c_i\leq 10^6$

题解

所有的期望问题都可以转化为求所有情况总和的问题，我们现在不妨进行一次转化，将其变为统计总和。

接下来我们将所有金库按照被mimic分隔的方式分为一些段，那么对于每个长度为$len$的段，其中金库的贡献系数分别为$1,2,3,\dots,len$。接下来我们不妨以此为基础，证明几个引理。

通过微扰法可以证明：对于任意两个段，若它们的长度差不小于$2$，则通过将一个数从大的移至小的可以使答案更小，因为所有段的长度都应至多相差1。

通过最简单的贪心可以证明，对于一个段内部，一定将所有价值的金库从大到小排序，然后按照$1,2,3,\dots,len$的顺序给其加上系数会使答案最小。

接下来我们便可以根据这两个引理写出一个$O(n^2)$的程序了：将最大的$k$个系数赋值为$0$，次大的$k$个系数为$1$，$\dots$，以此类推。值得注意的是，最后的几个数可能未必凑满$k$个，但是不需要特殊处理。

那么如何进行优化呢？我们注意到每次给连续的$k$个赋上相同的系数的步骤可以简化，直接利用前缀和乘上系数即可快速的计算答案。总的复杂度为$\sum \frac{n}{k}=n\log n$。可以优雅的通过本题。

Code

#include<bits/stdc++.h>
#define mod 998244353
using namespace std;
template<typename T>
inline void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
}
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	x*=f;
	return;
}	
template<typename T>
void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>=10) write(x/10);
	putchar(x%10+'0');
	return;
}
const int MAXN=300010;
int n;
long long c[MAXN];
long long pre[MAXN];
long long powmod(long long a,int b)
{
	if(b==0) return 1;
	if(b==1) return a;
	long long tmp=powmod(a,b>>1);
	tmp*=tmp,tmp%=mod;
	if(b&1) tmp*=a,tmp%=mod;
	return tmp;
}
int main()
{
	read(n);
	for(int i=1;i<=n;++i) read(c[i]);
	sort(c+1,c+n+1),reverse(c+1,c+n+1);
	for(int i=1;i<=n;++i) pre[i]=(pre[i-1]+c[i])%mod;
	for(int k=1;k<=n;++k)
	{
		long long ans=0;
		for(int i=k+1,j=1;i<=n;i+=k,++j) ans+=(pre[min(i+k-1,n)]-pre[i-1])*j%mod,ans%=mod;
		ans*=powmod(n,mod-2),ans%=mod;
		ans=(ans+mod)%mod;
		write(ans),putchar(' ');
	}
	putchar('\n');
	return 0;
}